Research Highlighted

A (somewhat outdated, sorry…) selection of some research contributions, including slides.

IJCAI Early Career Spotlight

I was selected for an early career spotlight talk at IJCAI’18, giving an overview of my research.

For more info, see the presentation of the accompanying paper.

Monte-Carlo Tree Search for Decentralized Decision Making on Robots

In this work, we introduce a way to use MCTS for decision making in ‘spatial task allocations problems’ and particularly tasks like autonomous warehousing. The main idea is that while heuristics as frequently employed in multirobot task allocation might not be sufficient to deal with highly dynamic worlds, they may be adequate to use as models of teammates.

Since then, Daniel Claes has also implemented this on the smartlab’s youbots:

Simulation-based Planning using Deep Q-learning for Traffic Light Control

Better traffic light control in urban settings could have great impact on quality of living. In some recent research I have been investigating the applicability of deep reinforcement learning techniques to improve traffic flow.

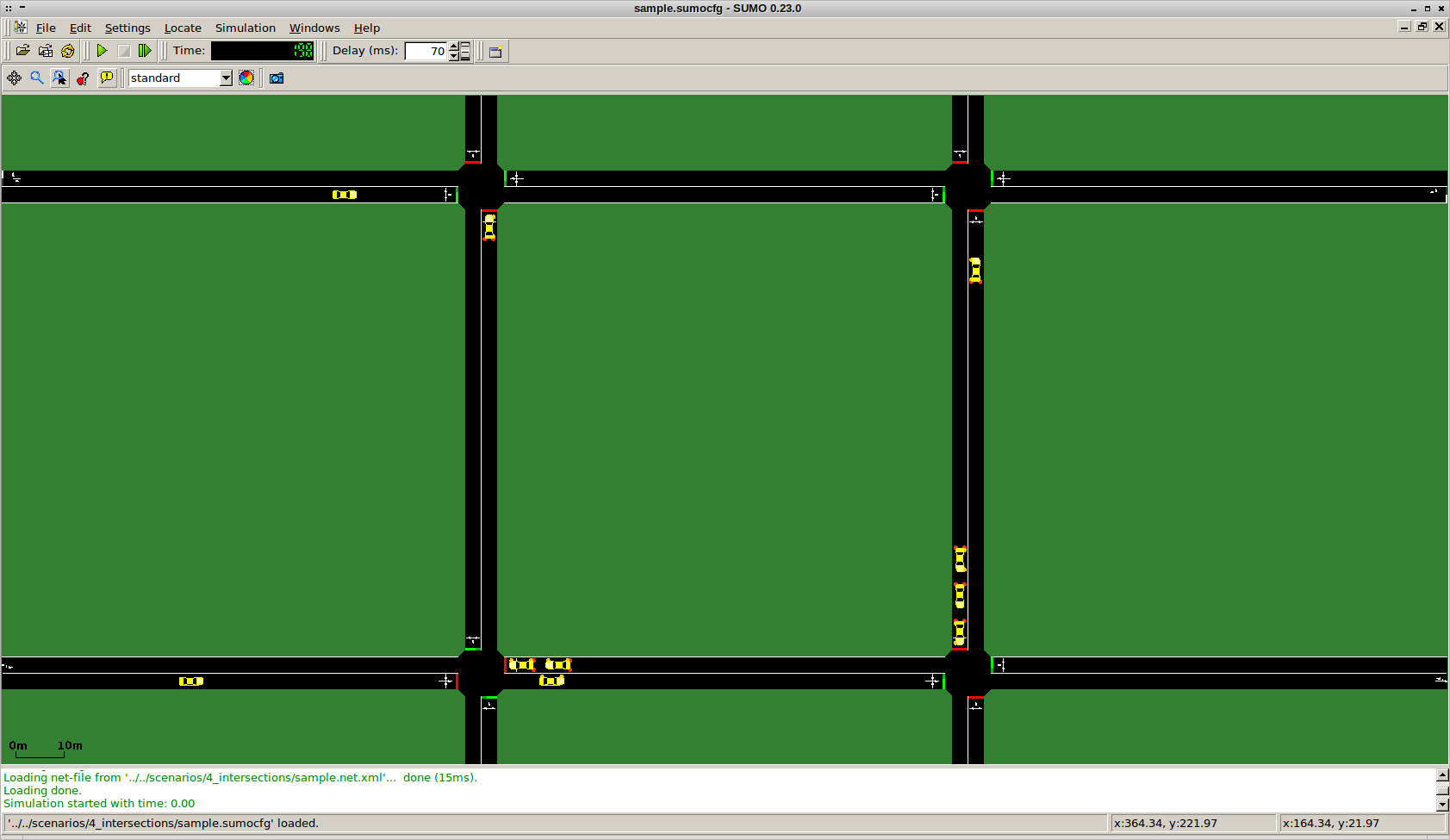
In particular, in her MSc project Elise van der Pol has shown that the DQN algorithm can be applied for the control of one and two intersection problems. The latter can than be used in a coordinated approach, by building on a variant of transfer planning (further described below). The results are quite exciting, as a video (link below) shows this new approach might allow for higher traffic densities without complete congestion, when compared to a state-of-the-art other coordination approach (the approach by Kuyer et al. 2008).

For more information, see…

Multiagent decision processes: Formal models for multiagent decision making

Multiagent systems are complex: they have complex interactions and can live in complex environments. In order to make any sense of them, much of my research focusses on formal models for multiagent decision making. These models include various extensions of the Markov decision process (MDP), such as multiagent MDPs (MMDPs), decentralized MDPs (Dec-MDPs), decentralized partially observable MDPs (Dec-POMDPs), partially observable stochastic games (POSGs), etc. I refer to the collection of such models as multiagent decision processes (MADPs).

Decentralized POMDPs

In particular, much of my research addresses the framework of decentralized POMDPs (Dec-POMDPs). A Dec-POMDP models a team of cooperative agents situated in an environment that they can only observe partially (e.g., due to limited sensors). To add to the complexity, each team member can only base its actions on its own observations.

If you want to learn about Dec-POMDPs, a good place to start might be these:

The book that Chris Amato and I wrote. Check it out here or at Springer.
Shorter, but also denser, is the book chapter that I wrote.
Some of the lectures I gave, see teaching materials

Alternatively, you may want to have a look at the first two chapters of my PhD Thesis, or check out the survey article by Seuken & Zilberstein (2008, JAAMAS).

Further pointers:

The Dec-POMDP book tries to give a clear explanation of the landscape of MADPs.
The MADP Software toolbox implements many MADPs and some of their solution methods.
The Dec-POMDP problem repository.

Advances in Optimal Solutions for Dec-POMDPs

The optimal solution of Dec-POMDPs is a notoriously hard problem. Yet, the field is making steady progress in solving larger POMDPs.

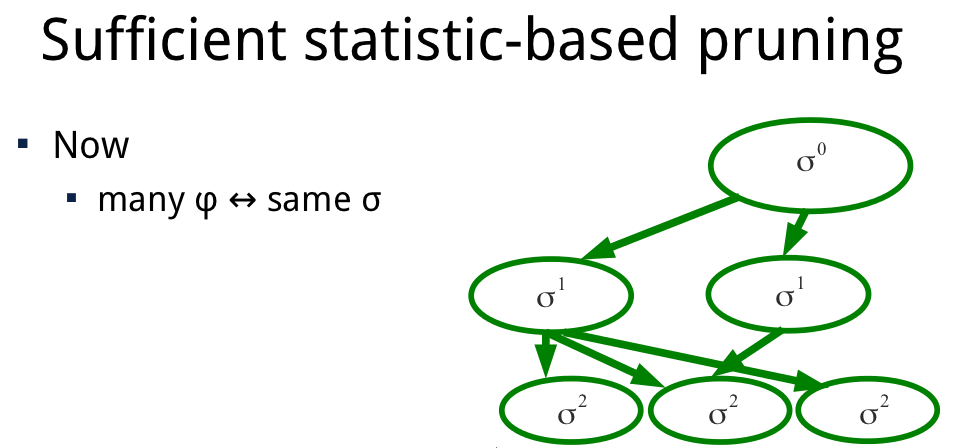
Incremental clustering and incremental expansion are two techniques that are introduced in our JAIR’13 article that have greatly expanded the range of problems that can be solved optimally. More recently, I found a reformulation of optimal value functions based on sufficient statistics that may enable more compact representations of those value functions and potentially can lead to speed ups.

For more information, see…

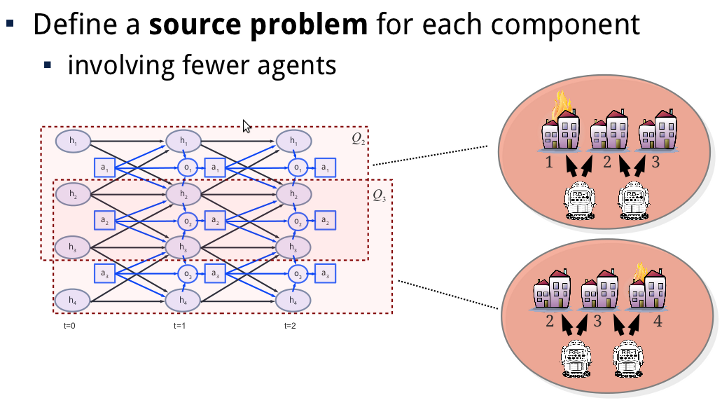
Approximate Solution of Factored Dec-POMDPs via Transfer Planning

In recent work we have introduced transfer planning, a method to compute a factored heuristic for factored Dec-POMDPs. By using this in a factored version of forward-sweep policy computation, we can scale to hundreds of agents.

The main idea behind transfer planning is that we approximate the original problem using a set of multiple abstractions, each involving subsets of agents. The value functions of these so-called source problems, can then be transfered to the original problem.

For more information, see…