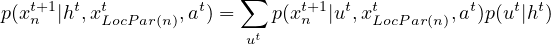(If you prefer PDF, look here)
About ‘Influence’
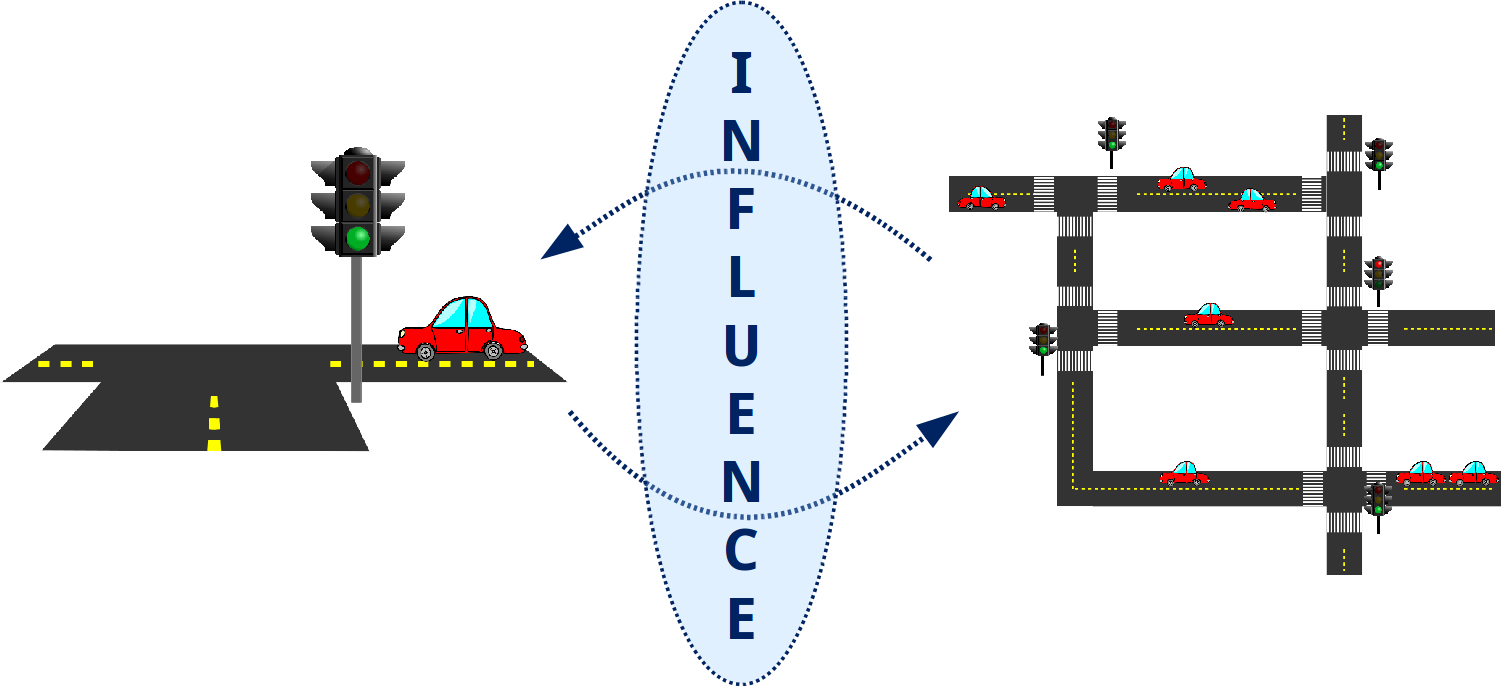
Abstraction is a key concept in AI. One could argue that the ability to focus on precisely the relevant aspects of a problem is a defining feature of intelligent behavior. How else can we make sense of such a complex place as the real world, consisting of trillions of objects, billions of people, and constantly changing configurations of these? However, even though in many cases it may be relatively easy to determine which factors are most important, it is not clear how to abstract away factors which are deemed less important: even if less important, they still have some influence.
In this blog post, we will try to give some of the intuitions behind influence-based abstraction (IBA), a form of state abstraction that eliminates entire state variables, also called (state) factors. IBA provides a formal description of doing abstraction in complex decision making settings, and makes links between reinforcement learning (RL) in partially observable settings, supervised learning, and causal inference. It splits a complex decision making problem into two separate problems: a local Markov (i.e., causal) decision making problem (e.g., reinforcement learning) and an influence prediction problem that can be addresses with supervised learning. Even though the influence-prediction problem introduces a dependence on the local history, this novel perspective offers many opportunities for efficient planning and learning in both single and multiagent settings.
The theory of influence-based abstraction as we will cover here was initially developed in [12], and elaborated upon in a recent JAIR paper [13]. The goal of this blog is to give a more high level description of the main concept, as well as how it relates to current trends.
1 The High Level Idea
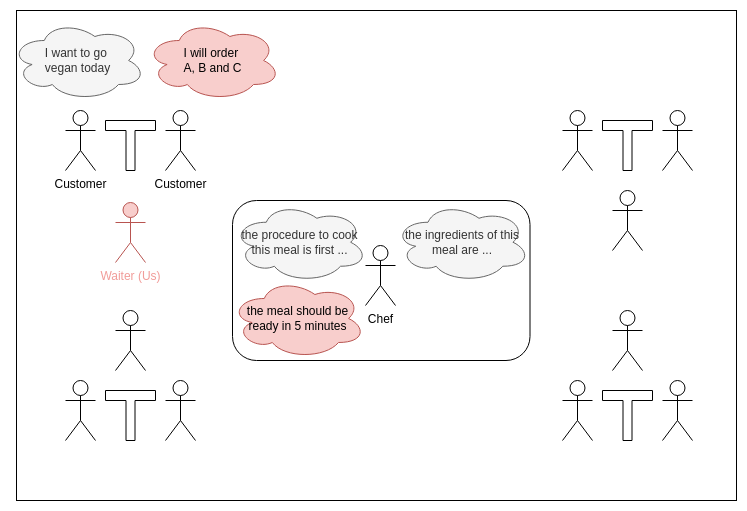
Imagine you have landed your first job as a waiter in a nice restaurant. As part of your job you will need to interact with customers, and coordinate with the chef, as well as any other waiters. Luckily for you, this does not mean that you know everything about them: you are not required to know or understand the customers’ preferences regarding footwear, nor do you need to understand exactly how the cook prepares the meal. As long as you can understand the preferences expressed about the food, and can anticipate the timing of the cook, you can go a long way on your first shift.
The above makes clear how abstraction can be critical for dealing with complex decision making problems. There are many types of abstraction [10], ranging from very specific ways of aggregating states, to general applications of function approximation. Here, we focus on the idea of influence-based abstraction, which originated from the multiagent planning community, [e.g., 1, 24, 16, 28, 25], but is a specific, principled, approach to the more general idea of state abstraction [e.g., 19, 8, 4, 9, 6], and hence also applies to single agent settings.
As an example, we can think of planning a trip to go ‘wadlopen’ (translates to: mud walking) in the beautiful Dutch Wadden Sea. During low tide, much of the sea falls dry and you can walk over the seabed from sand back to sand bank. Clearly, you want to plan your trip appropriately to avoid getting stuck on one! Fortunately, this is possible without fully predicting the exact height of the tide during every second of your trip, let alone reasoning about the exact interaction between water particles, moon and wind that gives rise to that. By merely predicting at what time the lowest parts of your route will become inaccessible, you can plan your trip.
These two examples make clear that, in many different complex decision problems, restricting our attention to appropriate parts of the problem might be sufficient as long as we are able to predict the influence (timing of the cook, time of routes being blocked) of all the other variables that we abstract away (cook’s state of mind, water particles interacting). This potentially huge simplification of the problem can lead to significant computational benefits.
2 Formalizing Influence-based Abstraction
Influence-based abstraction targets decision making in structured complex problems, that can be formalized as ‘factored POMDPs’. These are a special case of the partially observable Markov decision process (POMDP)—which itself is a standard framework for representing decision making problems with state uncertainty [7, 20]—in which the states consist of some number of state variables or factors. By making use of Bayesian networks to exploit the conditional independence between these factors, it is often possible to compactly represent the model (transitions, observations, and rewards) [2], as illustrated in Figure 2. We will refer to this as the ‘global’ model.
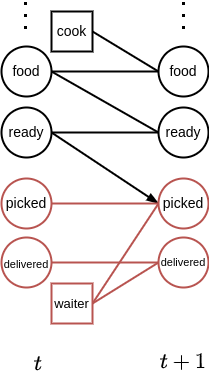
In much of the work we have done on influence-based abstraction, we assume that the global model is given and we ‘just’ want to plan for some number of time steps T. However, we typically have some motives (e.g., planning efficiency, storage size) to reduce the size of the problem by building an abstraction. E.g., while planning we do not want to consider the interaction between the moon and the water particles, even if we could model this quite accurately. However, we stress that the conceptual impact of this form of abstraction goes beyond just planning: it describes under what assumptions a good solution can be found when completely ignoring a large part of the original problem (whether we had the full model, or not).
In influence-based abstraction, our goal is to abstract away some set of state variables. We are interested in characterizing lossless abstractions—i.e., ones that do not lead to loss in task performance or value—and therefore will assume that we will only abstract away latent (i.e., non-observable) state variables, since throwing away actual observations can typically not be done without loss in value. A so-called local-form model specifies which variables we will abstract away. Specifically, a local-form model is a factored POMDP (or partially observable stochastic game in the multiagent case) that specifies:
- The modeled variables. These are the (important) variables that are explicitly represented in the ‘local model’ that the agent can use after abstraction. The ‘local state’ of the modeled variables at time step t will be denoted xlt.
- The non-modeled variables. These are the latent variables that are deemed less important. We want to avoid explicitly reasoning about these (but somehow still capture their ‘influence’).
To keep the exposition clear, we focus on the case where the local state xl is fully observable. However, this can be generalized as long as the local states include all the reward-relevant and observation-relevant variables, i.e. those state variables that are direct parents of the rewards and observations [13].
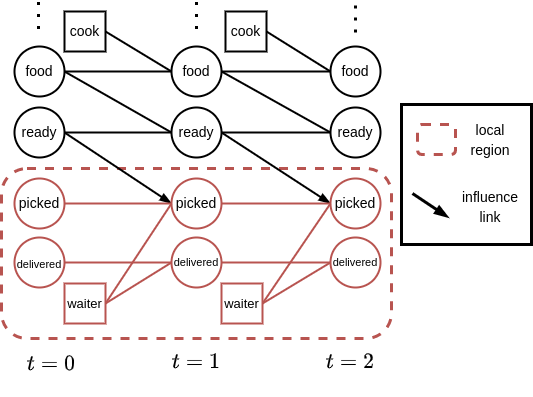
Now let us turn our attention to Figure 3. We want to ignore the non-modeled variables, but in order to predict the next local states (and specifically the variable ‘p’ in Figure 3) will need to reason about the arrows pointing into the local problem. We call the source of such an in-pointing arrow (the variable ‘r’ in Figure 3) an influence source, and will denote such sources with u. The variable ‘p’ in the local state is called an influence destination. Given this terminology, it may become apparent that, if we can predict the (probabilities of the) influence sources, then we can also predict the (probabilities of the) influence destinations. In other words, this enables us to do local planning.
This brings us to the main result of influence-based abstraction [13], which states that for a local-form model it is possible to construct a so-called influence-augmented local model, which is specified only over local variables without loss in value.
To accomplish this, such a model uses a representation, called an (exact) influence point, to predict the influence sources, which in turn is used to predict the influence destinations. Specifically, if we let ht denote the local history of local states and actions, then p(ut|ht) is the influence exerted at stage t and can be used to predict the probability of the influence destinations at the next time step t + 1. Alternatively, it is also possible to try to directly predict the influence destinations, see [13] for details. Of course, the other local variables just depend on their parents in the previous time step.
3 Differentiating Markovian vs Non-Markovian State Features
In this way, IBA provides a new perspective on decision making in such structured
problems: it allows us to split the local state into two types of local state variables
xl = 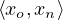 :
:
- The ones that behave Markovian, because all their parents are included in the local model. We will denote the state of these variables as xo (‘o’ stands for for “only locally affected” state variables).
- The ones that behave non-Markovian, because there is at least some variable u that we abstracted away that influences it. We let xn denote the state of such a non-Markovian (or “non-locally affected”) state variable.
To make this clear, note that the influence exerted at stage t, p(ut|ht), leads to an induced CPT for the influence destination xn at stage t + 1:
where LocPar(n) denotes the set of local variables that are parents of xn, and xLocPar(n)t denotes their value at stage t. Clearly, the dependence on the history reveals the non-Markov nature of xn.
At this point the reader may wonder how this is different from just thinking of the entire local problem as a POMDP: certainly, when conditioning on the history, one can directly predict the entire local state p(xlt+1|ht,at). However, such a perspective discards the structure in the problem, which is important for several reasons:
- Predicting the value of a single (or small set of) influence variable(s) might be much easier than predicting the full local state: it is lower dimensional and predicting less requires less information. E.g., when we go mud walking, we only need to reason about the amount of time since the last high tide to predict when parts of our route will get blocked. Predicting our precise progress requires much more information and is a more complex function. IBA formalizes this by defining the influence as p(ut|Dt) where Dt is a sufficient statistic of the local history ht (also called the “d-separating set” or “d-set”).
- Predicting the value of the Markovian variables xo, certainly is much easier, since we do not require any history dependence. E.g., when we go mud walking, we can predict the effect of taking a sip of water from our drinking bottle without even thinking about the tide, or how long ago we departed.
- Moreover, if we are in the learning setting, for such Markovian variables it will be much easier to learn causal models, which means that if dynamics of some parts (e.g., some state variables) of the problem change, we can still reuse other parts, as they would form a modular representation.
Of course, it might be that advanced POMDP reinforcement learning methods in the future can automatically discover this structure of two types of state variables, and that is a worthwhile research agenda. However, given that we now know this structure directly follows from relatively mild assumptions on weak coupling of processes, we propose to incorporate such knowledge (e.g., in the form of inductive biases) in methods the field develops in the future.
4 Compact and Approximate Influence Representations, and Learning Them
One thing to note about the expression for the induced CPT (1) is that p(ut|ht) captures the influence of the external part of the system for predicting xnt+1. The exact influence point (EIP) therefore is nothing more than the collection 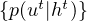 t=0T-1 of such conditional probabilities for different time steps (we assume a finite horizon in this exposition).
t=0T-1 of such conditional probabilities for different time steps (we assume a finite horizon in this exposition).
However, this immediately shows the intractability of such EIPs: the number of ht grows exponentially with t. By itself IBA does not lead to a free lunch: computing an exact influence in general is intractable.
To deal with this issue research so far has explored two directions:
- exploiting structure of special cases to find tractable representations.
- learning approximate influence points (AIPs).
The first direction is directly related to the idea of using a sufficient statistic Dt mentioned above. For instance, we can find compact exact statistics in a variant of the Planetary Exploration domain [28]. In this problem, we consider a mars rover that is exploring the planet and needs to navigate to a goal location. A satellite can compute a detailed navigation plan for the rover, making it easier to progress towards the goal. This is modeled with a ‘plan’ variable, indicating whether or not a plan has been generated already. Unfortunately, the satellite also has other tasks to take into consideration, so we do not know exactly if or when the plan will be available. This means that the rover needs to predict the probability p(asatellitet = plan|ht) that the satellite computes a plan, which will then flip the ‘plan’ available variable to true in the next time step. However, it turns out that in order to make this prediction, many things from the local history ht are irrelevant, and the rover can therefore represent a more compact p(asatellitet = plan|Dt). In this case, the history of the variable ‘plan’ is a sufficient statistic Dt, and given that in this problem the ‘plan’ variable can only turn true, Dt only needs to specify the time at which this switch happens.
Of course, in the general case, it might not be possible to find such compact exact statistics. In such a case, p(ut|ht) is both too large to represent due to the large number of local histories ht, as well as intractable to compute for each ht, computing p(ut|ht) is a hard inference problem. In this case, we might want to resort to trying to use approximate influence points (AIPs). The hope is that even though computing the exact influence (the exact distribution of the moment when some mud walking routes get blocked, which would depend on water particle interactions and position of moon) is intractable, a coarse prediction may still support very good decisions. Specifically, given that p(ut|ht) corresponds to a special case of sequence prediction problem, we may be able to use supervised learning methods to estimate 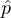 (ut|ht).
(ut|ht).
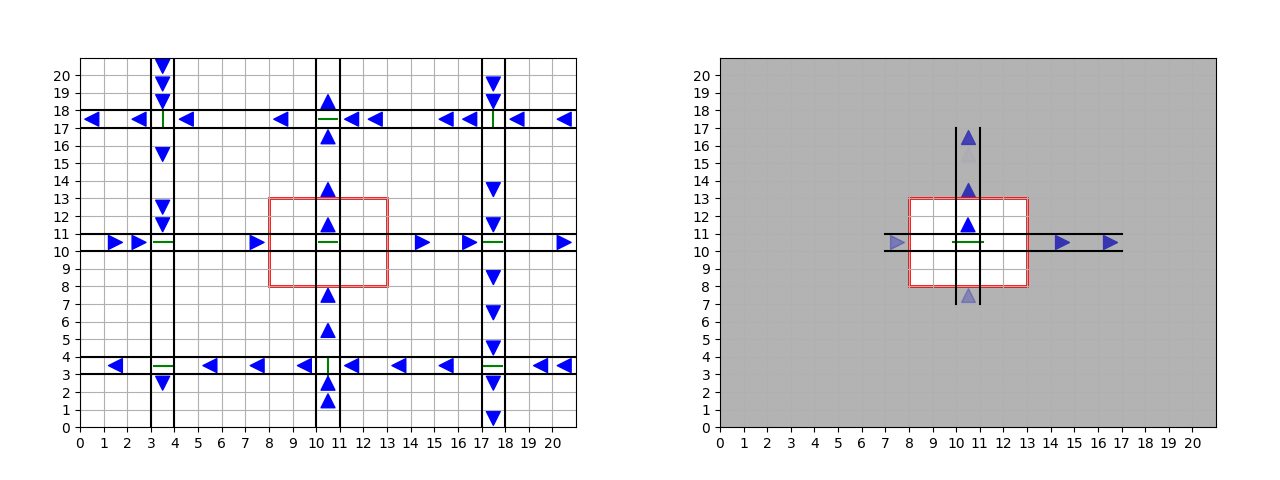
The idea is to use advances in machine learning to learn these approximations of
influence Î =  (ut|hy). The left hand side of Figure 4 represents a traffic scenario
with nine intersections, each one controlled by a traffic light. We take the perspective
of the central traffic light and the red square delimits its local model. Three learning
models have been employed to predict the influence corresponding to the distribution
of incoming and outgoing cars based only on the local model, as shown in Figure 5.
On the right side of Figure 4 we see how a model manages to predict quite
accurately the incoming and outgoing car flows. This supports the idea that
we can learn good influence approximations even for complex real-world
scenarios.
(ut|hy). The left hand side of Figure 4 represents a traffic scenario
with nine intersections, each one controlled by a traffic light. We take the perspective
of the central traffic light and the red square delimits its local model. Three learning
models have been employed to predict the influence corresponding to the distribution
of incoming and outgoing cars based only on the local model, as shown in Figure 5.
On the right side of Figure 4 we see how a model manages to predict quite
accurately the incoming and outgoing car flows. This supports the idea that
we can learn good influence approximations even for complex real-world
scenarios.
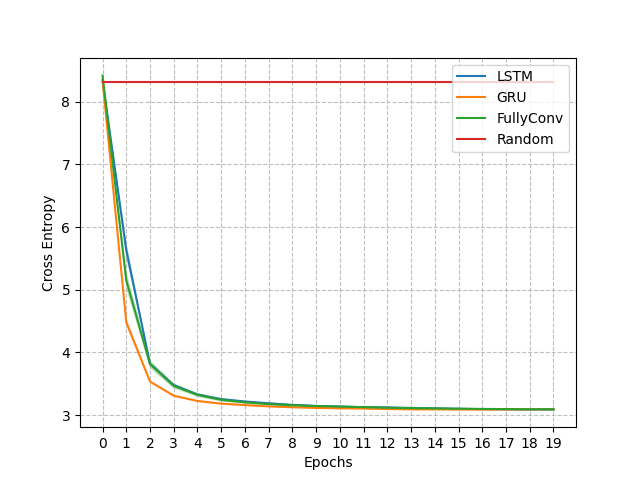
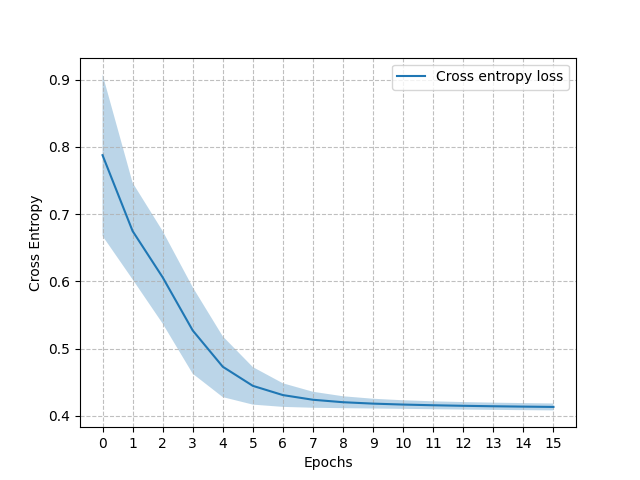
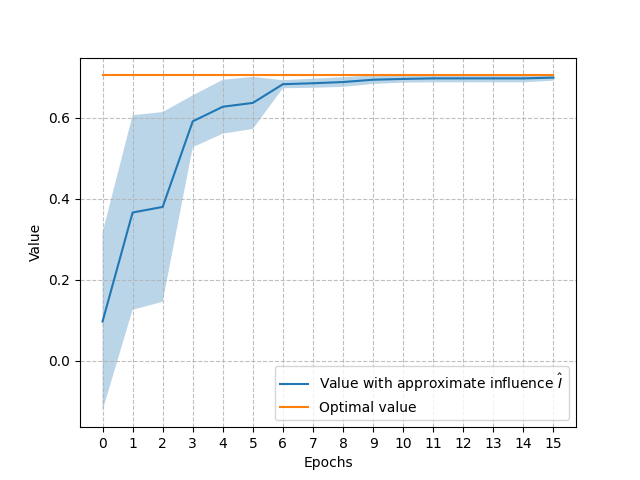
Moreover, we derived a loss bound that suggests that the supervised learning loss is well aligned with minimizing the value loss [3]. Figure 6 (left) shows the cross-entropy loss for the influence learning problem of the Mars Rover. The right side of the figure shows the value achieved by the policy learnt using the approximations of the influence corresponding to each epoch. As expected, during the first epochs we see the cross-entropy loss decreasing quickly and correspondingly an increase in the value achieved with the progressive approximations. When the cross-entropy loss converges to its minimum also the value approximates quite well the optimal value.
5 Further Implications
The idea of influence-based abstraction leads to, perhaps surprisingly many, connections and implications for (multiagent) decision making and learning. Full coverage is beyond the scope of this exposition, but we briefly mention a few further implications that have been explored.
For the case of a single agent that controls a part of a complex environment, there is evidence that learned AIPs can enable more efficient online planning [5]. The basic idea is that by using an AIP we can construct a local model that supports faster simulations than the full global model would, which thus provides a better trade-off in terms of speed vs accuracy.
In multiagent systems, research has explored influence search [1, 27, 26]. Here the idea is that, since many policies of one agent (e.g., cook) can lead to the same influence on another agent (e.g., waiter), the space of (joint) policies is much larger than the space of (joint) influences. Therefore, searching in the latter space can lead to significant speed-ups.
While the theory of IBA was developed in the context of planning, we believe that the insights it provides many implications for learning too. For instance, the possibility of lossless abstractions asserted by the theory of IBA directly implies that in multiagent settings, each agent could have an exact local (but history dependent) value function. As such this provides a possible explanation behind the success of value factorization in multiagent reinforcement learning such as VDNs [23] and Q-Mix [17].
The perspective of splitting a problem in Markovian and non-Markovian state variables can also be exploited in the context of Deep RL. In [22] we introduce a memory architecture for single-agent POMDP RL in which recurrent layers are only fed the variables in the agent’s observations that belong to the d-set. The rest of the observation variables (i.e. those that carry no information about hidden state variables) are simply processed by a feedforward neural network. This inductive bias is shown to improve convergence and learning speed when compared against standard recurrent architectures. More recently, Suau et al. [21] showed how the use of approximate IALS can speed up Deep RL in complex systems.
The theory of IBA may also lead to new insights when addressing problems where parts of the dynamics are non-stationary, i.e., may change over time [11]. The behavior of the tides, for example, may be different in summer and winter. As a non-stationarity of the system can always be seen as a latent variable that we did not account for, i.e. as a latent influence source, the theory of IBA is directly connected to non-stationary. problems.
Finally, we are also interested in exploring the relation of influence-based abstraction to ideas in causal inference [14, 15]. Specifically, in order to define our notion of ‘influence’ we have used sufficient statistics Dt that correspond to applying the backdoor criterion. In that way, it seems that ‘causally correct partial models’ as introduced in [18] actually correspond to a special case of influence-based abstraction.
6 Conclusions
In this text, we have given a high-level overview of influence-based abstraction, a technique that can construct abstracted local models of complex decision making problems. The main idea is that we can abstract away less important latent variables, as long as we still correctly capture their influence on the remaining local model. This constructed local model therefore will consist of two types of variables: “only locally affected variables” that behave Markovian, and the “non-locally affected” ones that have a non-Markovian dependence due to the influence of the variables abstracted away. Even though dealing with some non-Markovian variables can still be complex, we argue that it is easier than treating all variables as non-Markovian as one would do when just treating the resulting local model as a big POMDP. We provided some pointers to different ways in which this perspective of influence-based abstraction has made impact on single agent and multiagent problems, both in terms of planning and reinforcement learning. We expect that this structural insight will form the basis of many further improvements in large scale planning and reinforcement learning.
Acknowledgments
Thanks to Stefan Witwicki and Leslie Kaelbling, who co-invented the exact formulation of influence-based abstraction already in 2012. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 758824—INFLUENCE).

References
[1] R. Becker, S. Zilberstein, V. Lesser, and C. V. Goldman. Transition-independent decentralized Markov decision processes. In Proc. of the International Conference on Autonomous Agents and Multiagent Systems, pages 41–48, 2003.
[2] C. Boutilier, T. Dean, and S. Hanks. Decision-theoretic planning: Structural assumptions and computational leverage. Journal of Artificial Intelligence Research, 11:1–94, 1999.
[3] E. Congeduti, A. Mey, and F. A. Oliehoek. Loss bounds for approximate influence-based abstraction. In Proceedings of the Twentieth International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 377–385, May 2021.
[4] R. Dearden and C. Boutilier. Abstraction and approximate decision-theoretic planning. Artificial Intelligence, 89(1-2):219–283, 1997.
[5] J. He, M. Suau, and F. A. Oliehoek. Influence-augmented online planning for complex environments. In Advances in Neural Information Processing Systems 33, pages 4392–4402, Dec. 2020.
[6] L. P. Kaelbling and T. Lozano-Perez. Integrated robot task and motion planning in the now. Technical Report TR-2012-018, MIT CSAIL, 2012.
[7] L. P. Kaelbling, M. L. Littman, and A. R. Cassandra. Planning and acting in partially observable stochastic domains. Artificial Intelligence, 101(1-2):99–134, 1998.
[8] C. A. Knoblock. Generating Abstraction Hierarchies: An Automated Approach to Reducing Search in Planning. Kluwer Academic Publishers, Norwell, MA, USA, 1993. ISBN 0792393104.
[9] L. Li, T. J. Walsh, and M. L. Littman. Towards a unified theory of state abstraction for MDPs. In International Symposium on Artificial Intelligence and Mathematics, 2006.
[10] S. Mahadevan. Representation discovery in sequential decision making. In Proc. of the National Conference on Artificial Intelligence, 2010.
[11] A. Mey and F. A. Oliehoek. Environment shift games: Are multiple agents the solution, and not the problem, to non-stationarity? In Proceedings of the Twentieth International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 23–27, May 2021.
[12] F. A. Oliehoek, S. Witwicki, and L. P. Kaelbling. Influence-based abstraction for multiagent systems. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence (AAAI), pages 1422–1428, July 2012.
[13] F. A. Oliehoek, S. Witwicki, and L. P. Kaelbling. A sufficient statistic for influence in structured multiagent environments. Journal of Artificial Intelligence Research, pages 789–870, Feb. 2021. doi: 10.1613/jair.1.12136.
[14] J. Pearl. Causality: Models, reasoning and inference. 2000.
[15] J. Peters, D. Janzing, and B. Schölkopf. Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press, Cambridge, MA, USA, 2017.
[16] M. Petrik and S. Zilberstein. A bilinear programming approach for multiagent planning. Journal of AI Research, 35(1):235–274, 2009.
[17] T. Rashid, M. Samvelyan, C. Schroeder de Witt, G. Farquhar, J. Foerster, and S. Whiteson. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. ArXiv e-prints, 2018.
[18] D. J. Rezende, I. Danihelka, G. Papamakarios, N. R. Ke, R. Jiang, T. Weber, K. Gregor, H. Merzic, F. Viola, J. Wang, J. Mitrovic, F. Besse, I. Antonoglou, and L. Buesing. Causally Correct Partial Models for Reinforcement Learning. arXiv e-prints, art. arXiv:2002.02836, Feb. 2020.
[19] E. D. Sacerdoti. Planning in a hierarchy of abstraction spaces. Artificial Intelligence, 5(2):115–135, 1974.
[20] M. T. J. Spaan. Partially observable Markov decision processes. In M. Wiering and M. van Otterlo, editors, Reinforcement Learning: State of the Art, pages 387–414. Springer, 2012.
[21] M. Suau, J. He, M. T. Spaan, and F. A. Oliehoek. Speeding up deep reinforcement learning through influence-augmented local simulators. In Proceedings of the Twenty-First International Conference on Autonomous Agents and Multiagent Systems (AAMAS), May 2022. To appear.
[22] M. Suau de Castro, E. Congeduti, R. A. Starre, A. Czechowski, and F. A. Oliehoek. Influence-aware Memory for Deep Reinforcement Learning. arXiv e-prints, art. arXiv:1911.07643, Nov 2019.
[23] P. Sunehag, G. Lever, A. Gruslys, W. M. Czarnecki, V. F. Zambaldi, M. Jaderberg, M. Lanctot, N. Sonnerat, J. Z. Leibo, K. Tuyls, and T. Graepel. Value-decomposition networks for cooperative multi-agent learning based on team reward. pages 2085–2087, 2018.
[24] P. Varakantham, J.-y. Kwak, M. E. Taylor, J. Marecki, P. Scerri, and M. Tambe. Exploiting coordination locales in distributed POMDPs via social model shaping. In Proc. of the International Conference on Automated Planning and Scheduling, 2009.
[25] P. Velagapudi, P. Varakantham, P. Scerri, and K. Sycara. Distributed model shaping for scaling to decentralized POMDPs with hundreds of agents. In Proc. of the International Conference on Autonomous Agents and Multiagent Systems, 2011.
[26] S. Witwicki, F. A. Oliehoek, and L. P. Kaelbling. Heuristic search of multiagent influence space. In Proceedings of the Eleventh International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 973–981, June 2012.
[27] S. J. Witwicki. Abstracting Influences for Efficient Multiagent Coordination Under Uncertainty. PhD thesis, University of Michigan, Ann Arbor, Michigan, USA, 2011.
[28] S. J. Witwicki and E. H. Durfee. Influence-based policy abstraction for weakly-coupled Dec-POMDPs. In Proc. of the International Conference on Automated Planning and Scheduling, pages 185–192, 2010.